pystan：動的一般化線形モデル：ポアソン分布を仮定した例

実践Data Scienceシリーズ RとStanではじめるベイズ統計モデリングによるデータ分析入門 (KS情報科学専門書)

　「RとStanで始めるベイズ統計モデリングによるデータ分析入門」「実践編第5部第9章動的一般化線形モデル：ポアソン分布を仮定した例」を対象に，公開されているR，Stanのコードをpython，pystanのコードへと書き直した一例です。Stanの代わりにpystanを利用しています。

　この章では，ポアソン分布を仮定したDGLMの実装例が紹介されています。

　本ページでは公開されていない書籍の内容については一切触れません。理論や詳しい説明は書籍を参照してください。

　なお，こちらで紹介しているコードには誤りが含まれる可能性があります。内容やコードについてお気づきの点等ございましたら，ご指摘いただけると幸いです。

　（本ページにて紹介しているコードはgithubにて公開しています。）

DataAnalOji.hatena.sample/python_samples/stan/5-9-動的一般化線形モデル：ポアソン分布を仮定した例.ipynb at master · Data-Anal-Ojisan/DataAnalOji.hatena.sample

samples for my own blog. Contribute to Data-Anal-Ojisan/DataAnalOji.hatena.sample development by creating an account on GitHub.

分析の準備
モデルの推定
推定結果の図示
1. MCMCサンプルの取得
2. 個別のグラフの作成

分析の準備

パッケージの読み込み

　plotSSM関数についてはこちらをご参照ください。

import arviz
import pystan
import numpy as np
import pandas as pd

%matplotlib inline
import matplotlib.pyplot as plt
plt.style.use('ggplot')
plt.rcParams['font.family'] = 'Meiryo'
import seaborn as sns

# 自作のplotSSM関数を読み込み
from plotSSM import plotSSM

データの読み込み

fish_ts = pd.read_csv('5-9-1-fish-num-ts.csv')
fish_ts['date'] = pd.to_datetime(fish_ts['date'])
fish_ts.head(n=3)

図示

plt.figure(figsize=(10,5))
plt.plot(fish_ts['fish_num'], color='black')
plt.show()

モデルの推定

データの準備

data_list = dict(y=fish_ts['fish_num'],
                 ex=fish_ts['temperature'],
                 T=len(fish_ts))

モデルの推定

# stanコードの記述（5-8-1-dglm-binom.stan）
stan_code = '''
data {
  int T;        // データ取得期間の長さ
  vector[T] ex; // 説明変数
  int y[T];     // 観測値
}

parameters {
  vector[T] mu;       // 水準+ドリフト成分の推定値
  vector[T] r;        // ランダム効果
  real b;             // 係数の推定値
  real<lower=0> s_z;  // ドリフト成分の変動の大きさを表す標準偏差
  real<lower=0> s_r;  // ランダム効果の標準偏差
}

transformed parameters {
  vector[T] lambda;   // 観測値の期待値のlogをとった値
  
  for(i in 1:T) {
    lambda[i] = mu[i] + b * ex[i] + r[i];
  }

}

model {
  // 時点ごとに加わるランダム効果
  r ~ normal(0, s_r);
  
  // 状態方程式に従い、状態が遷移する
  for(i in 3:T) {
    mu[i] ~ normal(2 * mu[i-1] - mu[i-2], s_z);
  }
  
  // 観測方程式に従い、観測値が得られる
  for(i in 1:T) {
    y[i] ~ poisson_log(lambda[i]);
  }

}

generated quantities {
  // 状態推定値（EXP）
  vector[T] lambda_exp;
  // ランダム効果除外の状態推定値
  vector[T] lambda_smooth;
  // ランダム効果除外、説明変数固定の状態推定値
  vector[T] lambda_smooth_fix; 

  lambda_exp = exp(lambda);
  lambda_smooth = exp(mu + b * ex);
  lambda_smooth_fix = exp(mu + b * mean(ex));
}

'''

# モデルのコンパイル
stan_model = pystan.StanModel(model_code=stan_code)

# サンプリング
dglm_poisson = stan_model.sampling(data=data_list,
                                   seed=1,
                                   iter=8000,
                                   warmup=2000,
                                   thin=6,
                                   control={
                                       'adapt_delta': 0.99,
                                       'max_treedepth': 15
                                   },
                                   n_jobs=1)

推定されたパラメタ

print(
    dglm_poisson.stansummary(pars=["s_z", "s_r", "b", "lp__"],
                             probs=[0.025, 0.5, 0.975]))

Inference for Stan model: anon_model_3e7f96660af24f75fe7e27f7ed8f7131.
4 chains, each with iter=8000; warmup=2000; thin=6; 
post-warmup draws per chain=1000, total post-warmup draws=4000.

       mean se_mean     sd   2.5%    50%  97.5%  n_eff   Rhat
s_z    0.06  1.0e-3   0.03   0.02   0.05   0.14    985    1.0
s_r    0.17  4.0e-3   0.09   0.02   0.16   0.37    530   1.01
b      0.08  5.0e-4   0.02   0.04   0.08   0.12   1924    1.0
lp__ 980.59    1.39  24.71 941.01 977.14 1043.1    317   1.01

Samples were drawn using NUTS at Sun Sep 13 16:00:36 2020.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at 
convergence, Rhat=1).

参考：収束の確認

# 収束確認用のRhatのプロット関数
def mcmc_rhat(dataframe, column='Rhat', figsize=(5, 10)):
    plt.figure(figsize=figsize)
    plt.hlines(y=dataframe[column].sort_values().index,
               xmin=1,
               xmax=dataframe[column].sort_values(),
               color='b',
               alpha=0.5)
    plt.vlines(x=1.05, ymin=0, ymax=len(dataframe[column]), linestyles='--')
    plt.plot(dataframe[column].sort_values().values,
             dataframe[column].sort_values().index,
             marker='.',
             linestyle='None',
             color='b',
             alpha=0.5)
    plt.yticks(color='None')
    plt.tick_params(length=0)
    plt.xlabel(column)
    plt.show()


# 各推定結果のデータフレームを作成
summary = pd.DataFrame(dglm_poisson.summary()['summary'],
                       columns=dglm_poisson.summary()['summary_colnames'],
                       index=dglm_poisson.summary()['summary_rownames'])

# プロット
mcmc_rhat(summary)

print('hmc_diagnostics:\n',
      pystan.diagnostics.check_hmc_diagnostics(dglm_poisson))

hmc_diagnostics:
 {'n_eff': True, 'Rhat': True, 'divergence': True, 'treedepth': True, 'energy': True}

参考:トレースプロット

　’lp__’（log posterior）のトレースプロットは図示できないため除いています。

arviz.plot_trace(dglm_poisson, var_names=["s_z", "s_r"], legend=True)

参考：推定結果一覧

print(dglm_poisson.stansummary(probs=[0.025, 0.5, 0.975]))

　出力が非常に多いので割愛します。

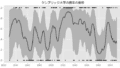
推定結果の図示

MCMCサンプルの取得

mcmc_sample = dglm_poisson.extract()

個別のグラフの作成

fig, ax = plt.subplots(3, 1, figsize=(15, 15))

p_all = plotSSM(mcmc_sample=mcmc_sample,
                time_vec=fish_ts['date'],
                obs_vec=fish_ts['fish_num'],
                state_name='lambda_exp',
                graph_title='状態推定値',
                y_label='釣獲尾数',
                axes=ax[0])

p_smooth = plotSSM(mcmc_sample=mcmc_sample,
                time_vec=fish_ts['date'],
                obs_vec=fish_ts['fish_num'],
                state_name='lambda_smooth',
                graph_title='ランダム効果を除いた状態推定値',
                y_label='釣獲尾数',
                axes=ax[1])

p_fix = plotSSM(mcmc_sample=mcmc_sample,
                time_vec=fish_ts['date'],
                obs_vec=fish_ts['fish_num'],
                state_name='lambda_smooth_fix',
                graph_title='気温を固定した状態推定値',
                y_label='釣獲尾数',
                axes=ax[2])
plt.show()